Z uvedbo virtualnih pomikov smo predpostavili, da bodo pomiki oz zacetne lege majhni in s tem je napaka tudi zanemarljivo majhna. Pogled na sliko 2 nam da vedeti, da pomiki pri simulaciji nikakor ne bodo majhni, saj sistem izgleda kot elasticni mehanizem. Linearizacijsko napako je mozno odpraviti tako, da se lokalni koordinatni sistem pomika skupaj z maso. Pri vsakem premiku v nov lokalnei koordinatni sistem masne tocke je potrebno popraviti zacetne pogoje vzbujanja. Tako uvedemo v v enacbe prostora stanj zacetna vzbujanja, ki so posledica prednapetih vzmeti.
S tem, ko uvedemo korekcijo linearizacijske napake, pa ne smemo
zanemariti numericnih napak, ki nastopajo pri sestevanju velikih
stevil z malimi. Ce to ne upostevamo, se lako pojavi tipicna
zaokrozitvena napaka, ki v skrajnem primeru vodi tudi k
nestabilnim izracunom. Zato bomo korigirali pozicijo masne tocke
le takrat, ko bo podmik katerekoli masne tocke vecji kot neka
predpisana vrednost 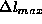
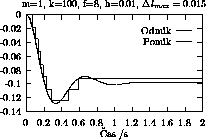
Na sliki 3 vidimo, kako za primer na sliki 1 premikamo koordinatni sistem skupaj z maso. Ker je sistem enodimenzionalen ni napake zaradi velikega odmika od zacetne lege. Tako mora biti odziv s pomikanjem enak odzivu brez pomikanja lokalnega koordinatnega sistema.
Za vsako masno tocko moramo kontrolirati odmike od lokalnega koordinatnega sistema. Vsakic ko kasksen pomik preseze dovoljeno vrednost ponovno izracunati matriko stanj z novimi smernimi kosinusi povezav med vozlisci. Potrebno je tudi pomniti zacetno pozicijo pomicnih vozlisc, ker moramo izracunati se prednapetje vzmeti, ki ji vstavimo ob prestavitivi lokalnega koordinatnega sistema v novo lego, kot vzbujanje s silo prednapetja v vektor u.
Nove vektorje vzbujanja u ob korekciji izracunamo kot
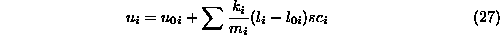
kjer je  smerni kosinus za ustrezno smer,
smerni kosinus za ustrezno smer, 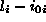 sprememba dolzine vzmeti. Indeks 0 pomeni zacetno stanje sistema.
Pozameznim vbujanjem je potrebno torej dodati silo prednapetja
vsake vzmeti, ki vpliva na maso v ustrezni smeri.
sprememba dolzine vzmeti. Indeks 0 pomeni zacetno stanje sistema.
Pozameznim vbujanjem je potrebno torej dodati silo prednapetja
vsake vzmeti, ki vpliva na maso v ustrezni smeri.
Omenjen pristop nam tako omogoca analizo mehanizmov in vecino translatornih sistemov.