Smerni kosinusi

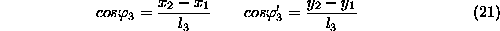
Poglejmo podrobneje enacbo (20). Pred vsakim virtualnim pomikom so si cleni zelo podobni. Iz trigonometrije vemo, da so to smerni kosinusi

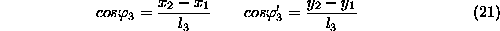
kar je razmerje dolzine v smeri zeljene koordinatne smeri in celotne dolzine daljice. V treh dimenzijah so smerni kosinusi podobni le da se dolzina povezave izracuna se z upostevanjem koordinate z.

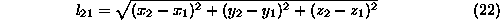
Zaradi krajsega pisanja oznacimo smerne kosinuse kot

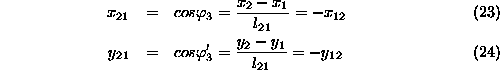
Ravnotezni enacbi prve mase (14) in (15) lahko zapisemo linearizirano

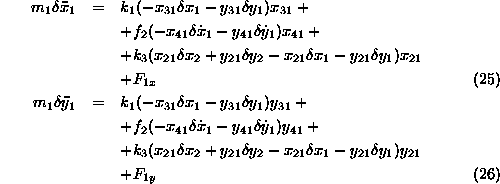
S primerno organizacijo lahko sistematicno napisemo enacbe stanja. Za primer na sliki 2 je potrebno napisati osem enacb stanja. To je pomik in hitrost v obeh dimenzijah (x,y) za obe masni tocki. Substitucije spremenljivk so podobne kot v enodimenzionalnem translatornem problemu. Izberimo take substitucije, da bodo v prvih stirih enacbah v desni diagonali same enice. Tako bodo pri sukcesivnem resevanju diferencialnih enacb prve stiri enacbe predstavljale pomike mas, naslednje stiri pa hitrosti.

Matrika 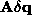prostora stanj brez upostevanje mas (11) izgleda v takole

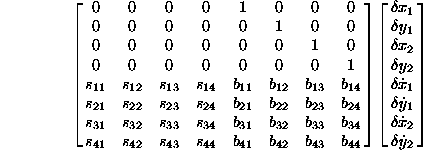
Napisimo clene podmatrik vzmeti in dusilk in uvedimo dodatne formalizme, tako da oznacimo konstante vzmeti in dusilk z indeksi vozlisc med katerimi se povezava nahaja. Primer:

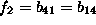
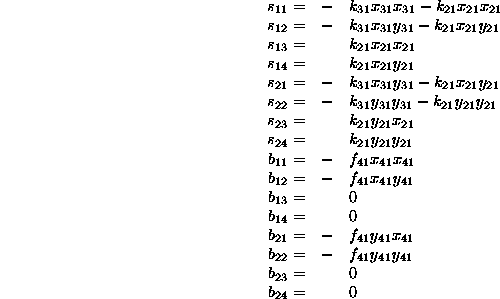
Ce podmatrike zapisemo tako , da zdruzimo vse koordinate posamezne mase vidimo, da so diagonalni elementi negativna vsota vsek povezav z obravnavano masno tocko, izvendiagonalni elementi pa predstavljajo povezave med posameznimi masami. Podmatrike so zaradi enakosti medsebojnih vplivov simetricne.

Algoritem gradnje matrike je lahko tak, da za vsako povezavo med dvema vozloma naredimo:

• Preverimo, ce je tip povezave dusilka, potem je gradnja podmatrike enaka vzmetem, le da se cleni pisejo v desno stran matrike A
• Prvi clen povezave pove, za ketero maso je potrebno dopisati diagonalne clene podmatrike
• Clene je potrebno napisati za vse koordinate. Cleni podvrstice se mnozijo s smernim kosimusom povezave v smeri vrstice
• Za vse podkolone je potrebno napisati clen, ki se mnozi s smernim kosinusom povezave v smeri kolone.
• Izvendiagonalni cleni so tisti, za katere je drugi clen povezave manjsi ali enak stevilu mas. Ta clen tudi pove, za katere maso je potrebno napisati povezavo. Tu smo predpostavili, da bomo vozlisca stevilcili tako, da bomo najprej oznacili mase, sele nato staticna vozlisca!
• Ce je drugi clen v povezavi tudi vozel, ki je gibljiv (masa) je potrebno dopisati diagonalne clene se za to maso.