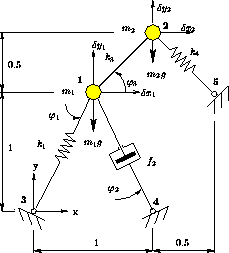
Obicajno vsaki masi za katero napisemo ravnotezne enacbe dolocimo lokalni koordinatni sistem z zacetni legi. Oglejmo si primer dvodimenzionalnega translatornega sistema na sliki 2.

Med masama je misljena toga povezava, ki pa jo lahko
nadomestimo z dovolj veliko togostjo vzmeti 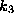 in si s tem
prihranimo dodatne analogije v modeliranju sistema.
in si s tem
prihranimo dodatne analogije v modeliranju sistema.
Tu za razliko od prejsnjega primera upostevamo lastno tezo masnih tock, ki se v prostoru stanj obravnava kot zunanje vzbujanje.
Prvi ravnotezni enacbi v lokalnem kartezijevem koordinatnem sistemu prve mase sta
S crko 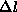 smo oznacili posamezne raztege vzmeti ali dusilke.
Za prvo vzmet je ta razteg enak
smo oznacili posamezne raztege vzmeti ali dusilke.
Za prvo vzmet je ta razteg enak
Vidimo, da razteg posamezne vzmeti ali dusilke s takim izborom koordinatnega sistema ni vec enostavna linearna funkcija, ki jo potrebujemo za zapis v prostoru stanj. Tudi drugacni koordinatni sistemi ne odpravijo te tezave, zato je potrebno uvesti dodatne poenostavitve.
Ce so pomiki dovolj majhni lahko pomik aproksimiramo s totalnim diferencialom. Kaj pomeni to: ,,dovolj majhni pomiki''? Diferencialno majhni pomiki so v primerjavi z dolzimi vzmeti ali dusilk zanemarljivi. V mehaniki pravimo takim pomikom virtualni pomiki. Po definiciji morajo biti taki pomiki majhni in seveda mozni. Za globalni kartezijev koordinatni sistem v treh dimenzijah je virtualni pomik

ali v splosnih koordinatah
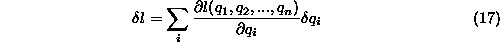
Realne pomike torej nadomestimo z virtualnimi. Da locimo med pomiki
jih dodatno oznacimo s crko  . Enacbo (15) tako
napisemo kot
. Enacbo (15) tako
napisemo kot
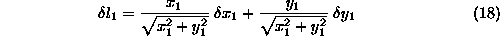
Dolzina tretje vzmeti je enaka

Virtualni pomik te vzmeti je torej odvisen od stirih virtuanih pomikov lokalnih koordinatnih sistemov masne tocke ena in dve