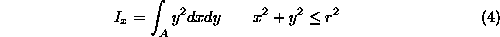
Ce uporabimo analogijo pri izracunu povrsine kroga in enacbo za vztranjostni moment opazimo, da je potrebno vse tocke, ki padejo znotraj kroga mnoziti se s kvadratom oddaljenosti od osi in tako dobimo popravljen program, ki nam racuna vztrajnostni moment kroga
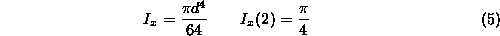
program Ix Kroga
n = 100000
a = 2.0 * 2.0
sn = 0.0
varx = 0.0
do 10 i = 1, n
x = 2.0 * ran2(idum) - 1.0
y = 2.0 * ran2(idum) - 1.0
if ((x*x + y*y) .lt. 1.0) then
sn = sn + y*y
varn = varn + y**4
endif
10 continue
print *, 'Vztr. moment kroga je:', sn/n*a
print *, 'Ocenjena napaka je:',
* a*sqrt((varn/n-(sn/n)**2)/n)
end
Ugotovimo lahko, da tocke, ki so blize teziscu ne prispevajo
bistveno k natancnosti izracuna, saj bistveni delez k vztrajnstnem
momentu prispevajo tocke, ki so bolj oddaljene od tezisca. Ugodno
bi torej bilo, ce bi pozornost posvetili oddaljenim tockam in ne
zgubljali casa okoli tezisca. V ta namen moramo bolj gosto sejati
tocke ob spodnjem in zgornjem robu.
Za integral (4) uvedimo substitucijo
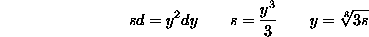
Integral se zdaj prevede na

kar je podobno izracunu povrsine, le da so se meje za y
spremenile iz 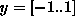 v
v 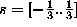 in s tem tudi
celotna povrsina omejitvenega pravokotnika, ki je zdaj
in s tem tudi
celotna povrsina omejitvenega pravokotnika, ki je zdaj
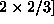 . S to substitucijo smo spremenili spektralno gostoto
generatorja belega suma v funkcijsko gostoto, pri kateri so tocke
ki so bolj oddaljene od tezisca tudi bolj gosto posejane. Za
testiranje meje pa uporabimo isto formulo kot prej, le da smo y
izracunali z inverzno transformacijo. Program s transformacijo
gostote je sledec:
. S to substitucijo smo spremenili spektralno gostoto
generatorja belega suma v funkcijsko gostoto, pri kateri so tocke
ki so bolj oddaljene od tezisca tudi bolj gosto posejane. Za
testiranje meje pa uporabimo isto formulo kot prej, le da smo y
izracunali z inverzno transformacijo. Program s transformacijo
gostote je sledec:
program Ix Kroga
n = 10000
a = (1.0 - (-1.0)) * (0.333 - (-0.333))
sn = 0.0
varx = 0.0
ss = 1.0/3.0 - (-1.0/3.0)
print *, -1.0**(1.0/3.0)
do 10 i = 1, n
x = 2.0 * ran2(idum) - 1.0
s = -1.0/3.0 + ss * ran2(idum)
y = (abs(3.0 * s))**(1.0/3.0)
if ((x*x + y*y) .lt. 1.0) then
sn = sn + 1
varn = varn + y**4
endif
10 continue
print *, 'Vztr. moment kroga je:', a*sn/n
print *, 'Ocenjena napaka je:',
* a*sqrt((varn/n-(sn/n)**2)/n)
end