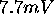Rezultati

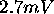Izmerjena je bila karakteristika diferencialnega transformatorja za polni obseg. Izmerjene izhodne napetosti brez kompenzacijskega vezja prikazuje tabela 1. V nicelni legi je imel diferencialni transformator 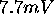nicelne napetosti, ki je bila kasneje kompenzirana z vezjem in izmerjena na .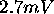

Slika 4 prikazuje karakteristiko diferencialnega transformatorja. Zaradi omejitev pri pomiku, je videti karakteristika dokaj linearna. Od najvecjega obsega bi bilo mozno izmeriti se kakih 0.5 mm vec, vendar so bile te meritve opuscene zaradi prikaza simetrije transformatorja.

 

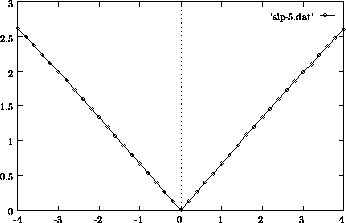
Za dolocitev najboljse premice, ki ima najmanjso napako v celotnem izmerjenem obsegu, lahko uporabimo regresijsko premico, ki ima enacbo

in je dolocena s steviloma a in b, ki ju izracunamo z metodo najmanjsih kvadratov, iz cesar izhaja:

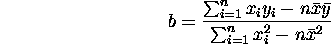
kjer je

in

Za podatke iz tabele 1 so bile izracunane naslednje vrednosti regresijske premice:

Negativna regresijska premica:
n =  21
x =  -42  y =  27.9367
xx =  114.8  yy =  50.4198
xy =  -76.077
mx =  -2  my =  1.33032
Regresijska premica: y = a + bx,  a =  0.018397  b =  -0.655961

Pozitivna regresijska premica:
n =  21
x =  42  y =  27.8987
xx =  114.8  yy =  50.2316
xy =  75.9332
mx =  2  my =  1.32851
Regresijska premica: y = a + bx,  a =  0.02099  b =  0.65376

Pripadajoci program za izracun regresijskih koeficientov je bil napisan v jeziku AWK:

BEGIN {
  init();
  prehod = 0;
}

END {
  print "\nPozitivna regresijska premica:"
  izpis();
}

{  /* glavna zanka */
  suma();

  if ($1 >= 0 && !prehod) /* $ */
    {
      print "\nNegativna regresijska premica:"
      izpis();
      init();
      suma();
      prehod++;
    } 
}

/* Inicializacija vsot */
function init()
{
  x = 0;
  y = 0;
  xx = 0;
  yy = 0;
  xy = 0;
  n = 0;
}

/* Vsote ene vrstice */
function suma() 
{
  x += $1;
  y += $2;
  xx += $1 * $1;
  yy += $2 * $2;
  xy += $1 * $2;
  n++;
  /* print "n:", n, " x = ", $1, " y = ", $2 */
}

/* Izpis vsote in regresijskih koeficientov */
function izpis() 
{
  print "n = ", n
  print "x = ", x, " y = ", y
  print "xx = ", xx, " yy = ", yy
  print "xy = ", xy
  mx = x/n; 
  my = y/n;
  print "mx = ", mx,  " my = ", my
  b = (xy - n*mx*my)/(xx - n*mx*mx);
  a = my - b*mx;
  print "Regresijska premica: y = a + bx,  a = ", a, " b = ", b 
}

 

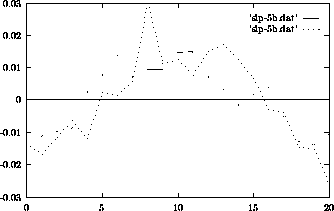
Iz slike 5 je razvidno, da obstaja ukrivljenost karaktereistike, ki je enaka tako za negatiivno, kot za pozitivno smer in ni le posledica napak pri meritvah.