
Slika 1: zgodnji modeli krivulj
Poročilo izdelal Andrej Auber ; Avgust - September , 1999.
Bezierjeve krivulje so zelo enostavne za izris, saj jih lahko izrišemo že na podlagi nekaj znanih kontrolnih točk. To poročilo vsebuje teoretične osnove in opis zgradbe in delovanja izdelanega programa za risanje Bezierjevih krivulj. Program omogoča risanje Bezierjeve krivulje n=3 v izometrični projekciji, na podlagi štirih podanih točk, oziroma njihovih zlepkov. Napisan je v FORTRAN - u, risanje krivulje pa je izvedeno s pomočjo PHIGS - a.
The Bezier curves are very comfortable way for drawing curves. They can be drawn from few known points. The report deals with theoretical bases of the Bezier curves. There are also included a running and a description of structure of a program for drawing the Bezier curves made by the author of this report. The program draws the Bezier curves n=3 in isometric projection on the base of 4 known control points and their composite. The program is written in FORTRAN, drawing of curves is made in PHIGS.
OPIS ZGRADBE IN DELOVANJA PROGRAMA
Avtomobilski proizvajalci so se dolgo časa ukvarjali s problemom, kako matematično popisati obliko avtomobilske karoserije. V začetku so si pomagali tako da so napenjali kovinske trakove okoli v desko zabitih žebljev.

S problemom, kako z modeli izdelane krivulje matematično popisati, se je ukvarjalo veliko inženirjev, med njimi tudi Bezier. Krivulje, ki jih uporabljamo v računalniških geometrijskih modelirnikih morajo imeti naslednje lastnosti:
Tem pogojem popolnoma ustrezajo Bernsteinovi polinomi, ki jih je Bezier izbral kot osnovo za svoje krivukje.
Bernsteinovi polinomi, ki jih je Bezier izbral kot osnovo za svoje krivulje so parametrični polinomi, katerih vrednost zavisi od vrednosti parametra, ki se nahaja na intervalu od [0,1]. Bernsteinovi polinomi imajo naslednji zapis:
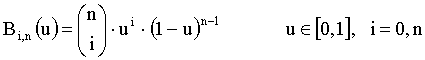
kjer so:
Pri stopnji n=2 dobimo naslednje polinome:
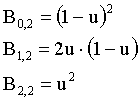
V uvodu naštetim pogojem ustrezajo že polinomi stopnje n=3, ki so naslednje oblike in zapisa:
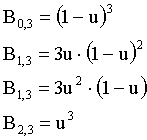
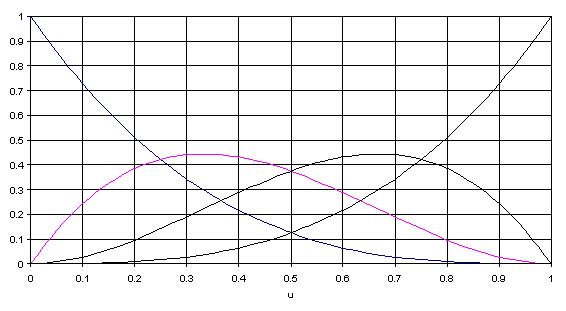
Iz Berensteinovih polinomov dobimo enačbo Bezierove krivulje:
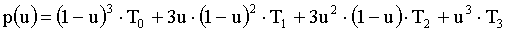
kjer so:
Vrednosti posameznih koordinat Bezierove krivulje pri določenem parametru, se izračunajo na naslednji način:
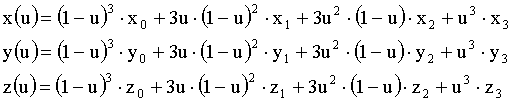
Iz enačb je razvidno, da za izris Bezierove krivulje reda n=3 potrebujemo 4 kontrolne točke. Za izris Bezierove krivulje reda n=4 potrebujemo 5 kontrolnih točk, za krivuljo reda n=5 potrebujemo 6 kontrolnih točk in tako naprej. Ker z večanjem stopnje narašča tudi stopnja polinomov in njihovo število, se s tem zelo poveča velikost matrike koeficientov Bernsteinovih polinomov. Tako je pri krivuljah reda n=3, matrika koeficientov reda 4 x 4 (16 elementov), pri krivuljah reda n=5, pa že 6 x 6 (36 elementov). Namesto krivulj višjega reda zato raje uporabljamo zlepke krivulj nižjih redov.
Prva lastnost Bezierovih krivulj je, da se ta v začetni in končni kontrolni točki tangentno dotika kontrolnega poligona, ki ga dobimo, če med seboj povežemo kontrolne točke, po vrsti od začetne do končne. Začetek in konec krivulje sta s tem fiksno določena, medtem ko s spreminjanjem položaja vmesnih kontrolnih točk spreminjamo obliko krivulje.
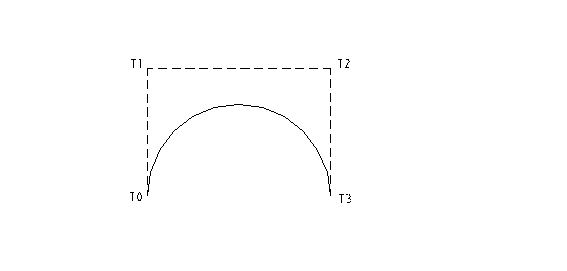
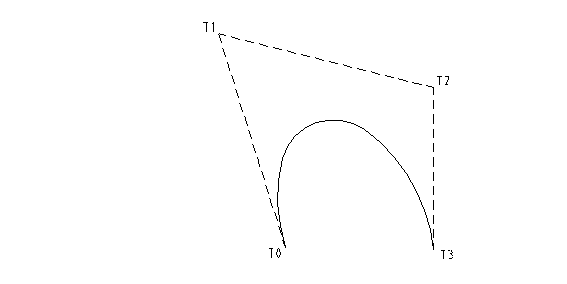
Naslednja pomembana lastnost, ki jo s pridom izkoriščamo, je invariantnost bezierjevih krivulj pri afinih preslikavah (rotaciji, translaciji, skaliranju). To lastnost dokažemo takole:
na znani točki Bezierove krivulje
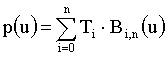
izvedemo preslikavo A
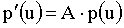
s katero dobimo nov položaj točke
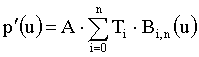
zaradi linearnosti lahko zapišemo tudi
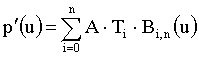
To pomeni da lahko preslikave izvajamo še preden izrišemo krivuljo. Tako namesto transformacije že izrisane krivulje, preslikamo kontrolne točke in na podlagi njihove nove slike narišemo krivuljo
Za uporabo v zlepkih, morata Bezierjevi krivulji, ki ju sestavljamo skupaj zadostiti naslednjima pogojema:
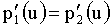
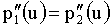
Da dobimo gladko nadaljevanje druge krivulje iz prve morata biti obe vsaj dvakrat odvedljivi, iz obeh zgornjih pogojev pa sledi, da morajo vse tri kontrolne točke ležati na isti premici.
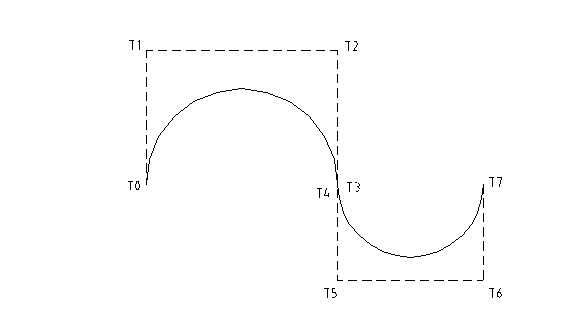
Program za izračun točk Bezierovih krivulj je napisan v FORTRAN - u, risanje krivulj pa je izvedeno s pomočjo emulacijske knjižnice PHIGS. Sam program je napisan kot celota v enem kosu, vendar ga lahko razdelimo v dva dela, v prvega, ki vsebuje algoritem za računanje točk Bezierove krivulje in v drugi del, ki te točke izriše na ekran. Program lahko riše Bezierjeve krivulje reda n=3 (potrebne so 4 kontrolne točke) in njihove zlepke, skupaj največ 6, za kar je potrebno podati koordinate 19 točk. Izrisana krivulja je na zaslonu prikazana v izometrični projekciji.
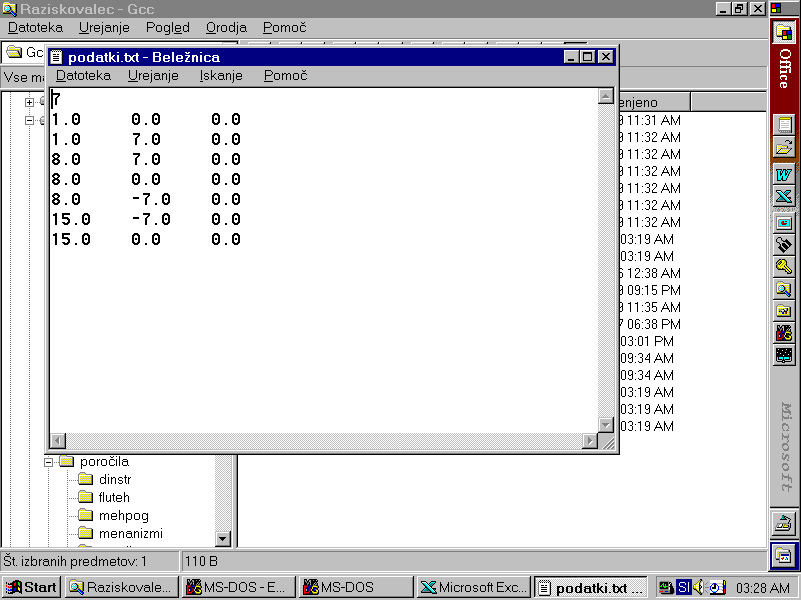
Program bere podatke (koordinate kontrolnih točk x, y in z) iz datoteke "Podatki.txt", v katerem je v prvi vrstici podano število vseh kontrolnih točk, ki mora biti celo in veliko najmanj 4. Za vsak naslednji zlepek je potrebno dodati še koordinate treh nadaljnih točk, torej 7, 10, 13 in tako naprej do 19, ki je največje možno število kontrolnih točk. V naslednji vrsticah so podane koordinate kontrolnih točk, v zaporedju kot si sledijo pri izrisu. V vsaki vrstici se nahajajo koordinate ene točke. Na prvem mestu v vrstici za "x" os, nato za "y" in v zadnjem stolpcu za "z" os. Vse vrednosti koordinat morajo biti posane z decimalno piko, četudi bi bila cela števila.
Algoritem izračuna točk Bezierjeve krivulje je prikazan v naslednjem diagramu poteka:
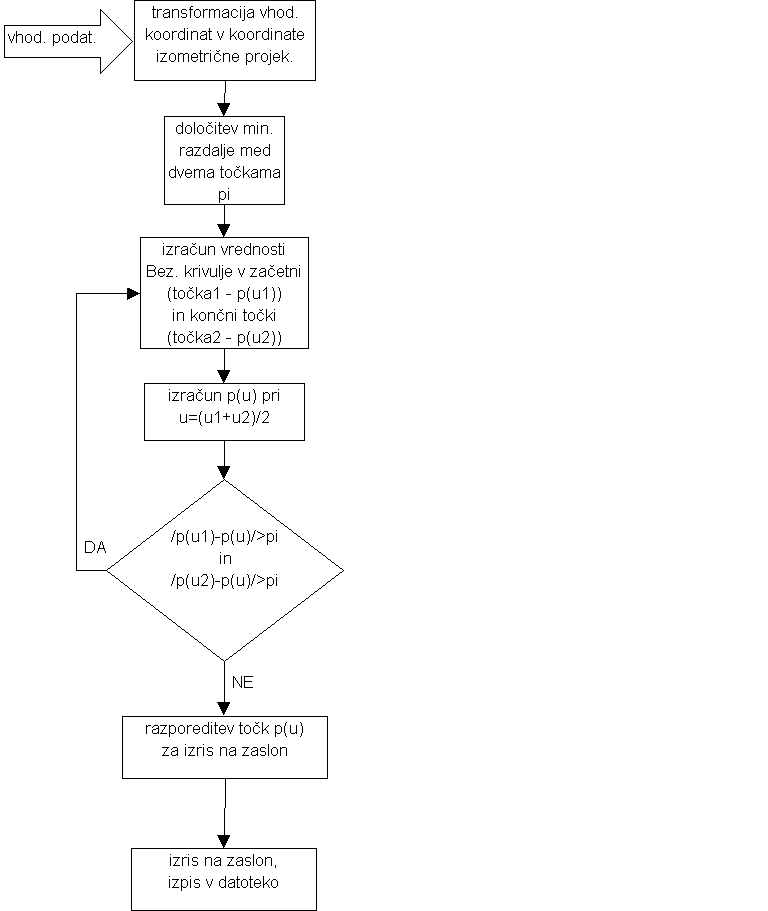
Prva funkcija v algoritmi je transformacija podanih koordinat, v koordinate izometrične projekcije. Iz podanih prostorskih koordinat je potrebno izračunati ravninsko projekcijo, ki je enaka pogledu na zaslonu. Vrednosti novih koordinat dobimo po naslednjih enačbah:
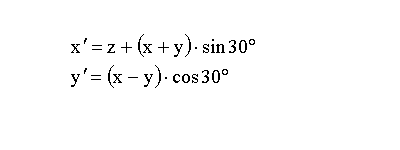
Druga funkcija v algoritmu je namenjena izračunu minimalne še dovoljene razdalje med točkami. Ta ne sme biti prevelika, ker bi bila izrisana krivulja preveč stopničasta, prav tako ni smiselo vzeti prekratko razdaljo, ker se s tem poveča število računskih točk. Mejna vrednost zavisi od največje razdalje med kontrolnimi točkami in velikosti ter resolucije zaslona.
Tretji najobširnejši del algoritma predstavlja izračun točk Bezierjeve krivulje. Računanje točk se izvaja z razpolavljanjem vrednosti parametra dveh točk. Tako najprej izračunamo koordinate začetne točke (parameter u=0) in končne točke (u=1). Nato vrednost parametra razpolovimo in izračunamo koordinate točk pri u=1/2. Potem se izračunta točki pri u=1/4 in u=3/4, in tako naprej. Pri tem se vsakokrat preverta razdalj od nove izračune točke do obeh sosednjih po vrednosti parametra.Če je razdalja med na novo izračunano in sosednjo točko manjša od minimalne dovoljene, se računanje novih točk na tistem odseku preneha. Računanje se še vedno nadaljuje vendar le na odsekih, kjer so si točke dovolj narazen.
Za izris je potrebno izračunane točke še urediti po vrednosti parametra od najmanjšega (začetne točke) do največjega (končne točke). V primeru da smo programu podali kontrolne točke zlepka, se ves postopek ponovi kot pri prvih štirih kontrolnih točkah.
Rezultati izračuna so vidni v obliki izrisa krivulje na zaslon, kakor tudi zapisa že urejenih točk v datoteko "rezultat.txt". V to datoteko se zapišejo vse vrednosti točk, ki so bile uporabljene za izris na zaslon.
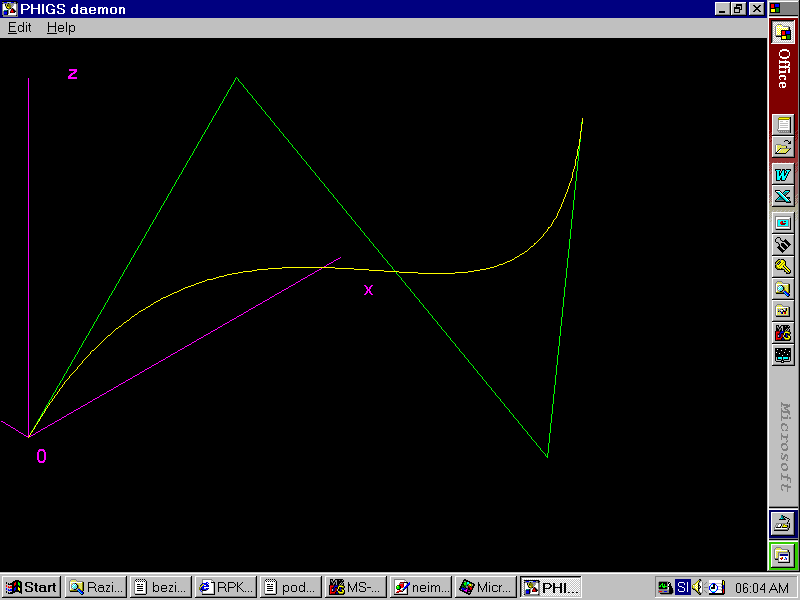
V nadaljevanju je predstavljenih nekaj primerov izrisa Bezierjevih krivulj z izdelanim programom.
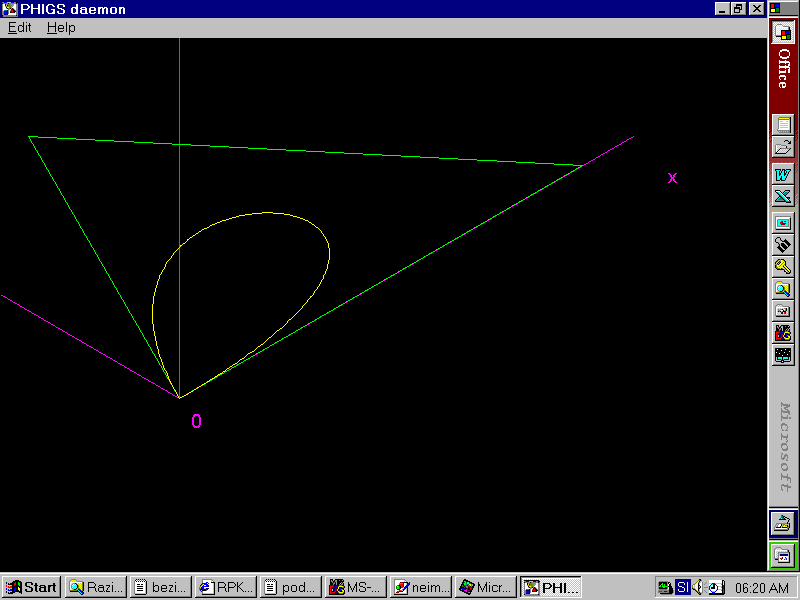
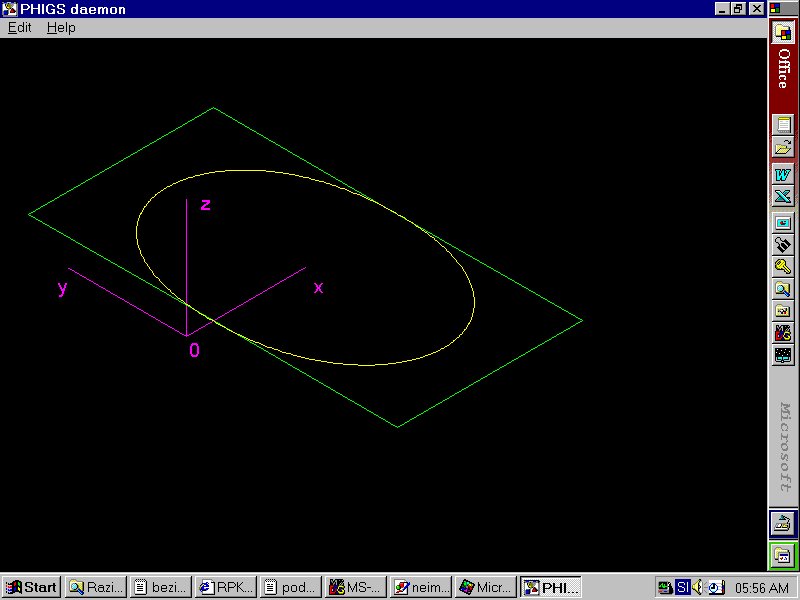
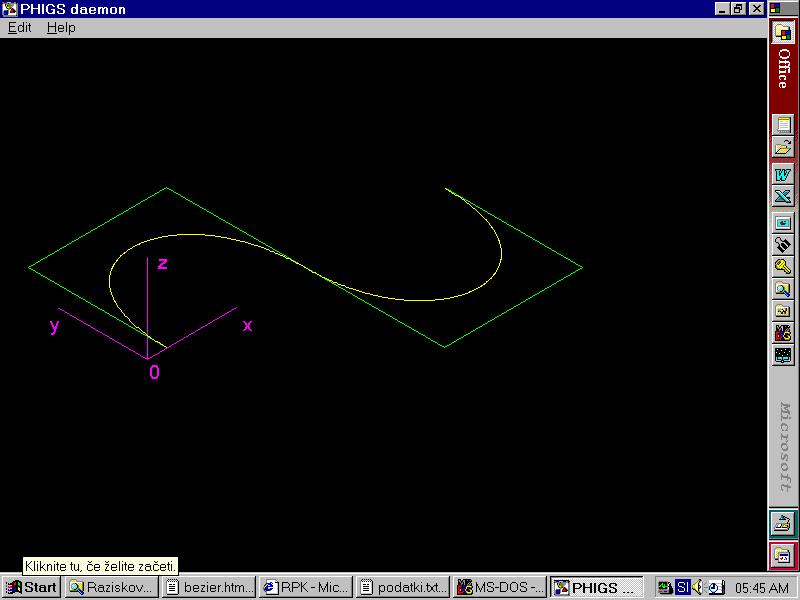
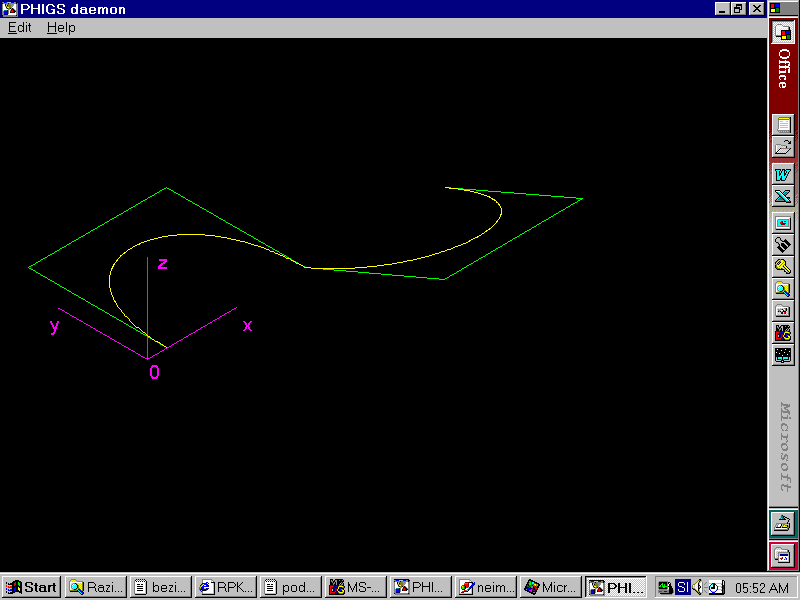
V zadnjem primeru je dobro vidno, da je v primeru zlepkov potrebno paziti pri izbiri kontrolnih točk. Če na mestu stičišča vse tri točke ne nahajajo na isti premici, se na krivulji pojavi stopnica.
Bezierjeve krivulje so najenostavnejša oblika krivulj, ki se uporablja v računalniških geometrijskih modelirnikih. Vzrok temu je prav gotovo enostavno definiranje krivulje s kontrolnimi točkami, kakor tudi sorazmerna enostavnost programiranja. Slabost bezierovih krivulj je ta, da moramo kontrolno točko prestaviti za kar veliko razdaljo, če želimo krivuljo bolj izrazito nagniti v določeno smer.
Izbrani algoritem, ki je bil uporabljen za izračun točk bezierjevih krivulj, ni ravno najbolj idealen, saj zahteva, kar nekaj spomina, ker si mora računalnik izračunane vrednosti zapomniti in zapisati v matriko, zaradi kasnejšega razvrščanja točk po velikosti parametra. Zelo enostaven algoritem bi bil možen, če bi točke računali korakoma od začetka do konca s spreminjanjem parametra za določeno vrednost. Slabost tega postopka je, da se nam pozicije kontrolnih točk spreminjajo in tudi razdalje med njimi. S tem se spreminjajo tudi vrednosti parametrov, pri katerih se nam splača računati točke krivulje. Namesto pomnjenja izračunanih vrednosti v matričnem zapisu, bi bil možen zapis vseh vrednosti v obliki enodimenzijskega polja, kar bi omogočalo tako povečanje števila zlepkov, ki bi jih lahko risali, kot tudi natančnost risanja krivulje.